Задача №33 (Из учебника С.А. Абрамов, Г.Г. Гнездилова, Е.Н. Капустина, М.И. Селюн; Вологда 2000г.)
Даны действительные числа х, у. Получить:
а) max (x, y);
б) min (x, y);
в) max (x, y) , min (x, y).
Скачать решение на языке: TPascal
Задача №34 (Из учебника С.А. Абрамов, Г.Г. Гнездилова, Е.Н. Капустина, М.И. Селюн; Вологда 2000г.)
Даны действительные числа x, y, z. Получить:
а) max (x, y, z);
б) min (x, y, z), max(x, y, z).
Скачать решение на языке: TPascal
Задача №35 (Из учебника С.А. Абрамов, Г.Г. Гнездилова, Е.Н. Капустина, М.И. Селюн; Вологда 2000г.)
Даны действительные числа x, y, z. Вычислить:
а) max (x + y + z, xyz);
б) min^2 (x + y + z/2, xyz) +1.
Скачать решение на языке: TPascal
Задача №36 (Из учебника С.А. Абрамов, Г.Г. Гнездилова, Е.Н. Капустина, М.И. Селюн; Вологда 2000г.)
Даны действительные числа a, b, c. Проверить, выполняются ли неравенства a < b < c.
Скачать решение на языке: TPascal
Задача №37 (Из учебника С.А. Абрамов, Г.Г. Гнездилова, Е.Н. Капустина, М.И. Селюн; Вологда 2000г.)
Даны действительные числа a, b, c. Удвоить эти числа, если a ≥ b ≥ c , и заменить их абсолютными значениями, если это не так.
Скачать решение на языке: TPascal
Задача №38 (Из учебника С.А. Абрамов, Г.Г. Гнездилова, Е.Н. Капустина, М.И. Селюн; Вологда 2000г.)
Даны действительные числа х, у. Вычислить z:

Скачать решение на языке: TPascal
Задача №39 (Из учебника С.А. Абрамов, Г.Г. Гнездилова, Е.Н. Капустина, М.И. Селюн; Вологда 2000г.)
Даны два действительных числа. Вывести первое число, если оно больше второго, и оба числа, если это не так.
Скачать решение на языке: TPascal
Задача №40 (Из учебника С.А. Абрамов, Г.Г. Гнездилова, Е.Н. Капустина, М.И. Селюн; Вологда 2000г.)
Даны два действительных числа. Заменить первое число нулем, если оно меньше или равно второму, и оставить числа без изменения в противном случае.
Скачать решение на языке: TPascal
Задача №41 (Из учебника С.А. Абрамов, Г.Г. Гнездилова, Е.Н. Капустина, М.И. Селюн; Вологда 2000г.)
Даны три действительных числа. Выбрать из них те, которые принадлежат интервалу (1, 3).
Скачать решение на языке: TPascal
Задача №42 (Из учебника С.А. Абрамов, Г.Г. Гнездилова, Е.Н. Капустина, М.И. Селюн; Вологда 2000г.)
Даны действительные числа x, y (x ≠ y). Меньшее из этих двух чисел заменить их полусуммой, а большее – их удвоенным произведением.
Скачать решение на языке: TPascal
Задача №43 (Из учебника С.А. Абрамов, Г.Г. Гнездилова, Е.Н. Капустина, М.И. Селюн; Вологда 2000г.)
Даны три действительных числа. Возвести в квадрат те из них, значения которых неотрицательны.
Скачать решение на языке: TPascal
Задача №44 (Из учебника С.А. Абрамов, Г.Г. Гнездилова, Е.Н. Капустина, М.И. Селюн; Вологда 2000г.)
Если сумма трех попарно различных действительных чисел x, y, z меньше единицы, то наименьшее из этих чисел заменить полусуммой двух других; в противном случае заменить меньшее из х и у полусуммой двух оставшихся значений.
Скачать решение на языке: TPascal
Задача №45 (Из учебника С.А. Абрамов, Г.Г. Гнездилова, Е.Н. Капустина, М.И. Селюн; Вологда 2000г.)
Даны действительные числа a, b, c, d. Если a ≤ b ≤ c ≤ d, то каждое число заменить наибольшим из них; если a>b>c>d, то оставить без изменения; в противном случае все числа заменяются их квадратами.
Скачать решение на языке: TPascal
Задача №46 (Из учебника С.А. Абрамов, Г.Г. Гнездилова, Е.Н. Капустина, М.И. Селюн; Вологда 2000г.)
Даны действительные числа x, y. Если х и у отрицательны, то каждое значение заменить его модулем; если отрицательно только одно из них, то оба значения увеличить на 0.5; если оба значения неотрицательны и ни одно из них не принадлежит отрезку [0.5, 2.0], то оба значения уменьшить в 10 раз; в остальных случаях х и у оставить без изменения.
Скачать решение на языке: TPascal
Задача №47 (Из учебника С.А. Абрамов, Г.Г. Гнездилова, Е.Н. Капустина, М.И. Селюн; Вологда 2000г.)
Даны действительные положительные числа x, y, z. а) Выяснить существует ли треугольник с длинами сторон x, y, z. б) Если треугольник существует, то ответить – является ли он остроугольным.
Скачать решение на языке: TPascal
Задача №48 (Из учебника С.А. Абрамов, Г.Г. Гнездилова, Е.Н. Капустина, М.И. Селюн; Вологда 2000г.)
Даны действительные числа a, b, с (а ≠ 0). Выяснить, имеет ли уравнение аx^2 + bx+ c = 0 действительные корни. Если действительные корни имеются, то найти их. В противном случае ответом должно служить сообщение, что действительных корней нет.
Скачать решение на языке: TPascal
Задача №49 (Из учебника С.А. Абрамов, Г.Г. Гнездилова, Е.Н. Капустина, М.И. Селюн; Вологда 2000г.)
Дано действительное число h. Выяснить, имеет ли уравнение ax^2 + bx+ c = 0 действительные корни, если:


Если действительные корни существуют, то найти их. В противном случае ответом должно служить сообщение, что действительных корней нет.
Скачать решение на языке: TPascal
Задача №50 (Из учебника С.А. Абрамов, Г.Г. Гнездилова, Е.Н. Капустина, М.И. Селюн; Вологда 2000г.)
Даны действительные числа a1, b1, c1, a2, b2, c2. Выяснить, верно ли, что a1*b2 - a2*b1 ≥ 0.0001 , и если верно, то найти решение системы линейных уравнений:
a1*x + b1*y + c1 = 0
a2*x + b2*y + c2 = 0
(при выполнении выписанного неравенства система заведомо совместна и имеет единственное решение).
Скачать решение на языке: TPascal
Задача №51 (Из учебника С.А. Абрамов, Г.Г. Гнездилова, Е.Н. Капустина, М.И. Селюн; Вологда 2000г.)
Даны действительные числа a , b , c ( a ≠ 0). Полностью исследовать биквадратное уравнение ax^4 + bx^2 + c = 0, т. е. если действительных корней нет, то должно быть выдано сообщение об этом, иначе должны быть выданы два или четыре корня.
Скачать решение на языке: TPascal
Задача №52 (Из учебника С.А. Абрамов, Г.Г. Гнездилова, Е.Н. Капустина, М.И. Селюн; Вологда 2000г.)
Даны действительные числа a , b , c , d , s , t , u ( s и t одновременно не равны нулю). Известно, что точки ( a , b ) и ( c , d ) не лежат на прямой l , заданной уравнением sx + ty + u = 0 . Прямая l разбивает координатную плоскость на две полуплоскости. Выяснить, верно ли, что точки ( a , b ) и ( c , d ) принадлежат разным полуплоскостям*). *) В этой задаче, как и в ряде следующих задач, надо воспользоваться тем, что две точки ( a , b ) и ( c , d ) , не лежащие на прямой, определяемой уравнением sx + ty + u = 0 , принадлежат одной полуплоскости, если sa + tb + u и sc + td + u – числа одного знака. Справедлив и более общий факт: если уравнение F ( x , y ) = 0 определяет прямую иликривую, разбивающую координатную плоскость на две части, то точки ( a , b ) и ( c , d ) , не лежащие на этой линии, принадлежат одной и той же части плоскости, если F(a , b) и F(c , d) – числа одного знака.
Скачать решение на языке: TPascal
Задача №53 (Из учебника С.А. Абрамов, Г.Г. Гнездилова, Е.Н. Капустина, М.И. Селюн; Вологда 2000г.)
Даны действительные числа a , b , c , d , e , f , g , h . Известно, что точки ( e , f ) и ( g , h ) различны. Известно также, что точки ( a , b ) и ( c , d ) не лежат на прямой l , проходящей через точки ( e , f ) и ( g , h ). Прямая l разбивает координатную плоскость на две полуплоскости. Выяснить, верно ли, что точки ( a , b ) и ( c , d ) принадлежат одной и той же полуплоскости*). *) В этой задаче, как и в ряде следующих задач, надо воспользоваться тем, что уравнением прямой, проходящей через две различные точки ( e , f ) и ( g , h ) , является уравнение ( x − e )( h − f ) − ( y − f )( g − e ) = 0 .
Скачать решение на языке: TPascal
Задача №54 (Из учебника С.А. Абрамов, Г.Г. Гнездилова, Е.Н. Капустина, М.И. Селюн; Вологда 2000г.)
Даны действительные числа x 1 , x 2 , x 3 , y 1 , y 2 , y 3 . Принадлежит ли начало координат треугольнику с вершинами ( x 1 , y 1 ), ( x 2 , y 2 ), ( x 3 , y 3 )?
Скачать решение на языке: TPascal
Задача №55 (Из учебника С.А. Абрамов, Г.Г. Гнездилова, Е.Н. Капустина, М.И. Селюн; Вологда 2000г.)
Даны действительные положительные числа a , b , c , d . Выяснить, можно ли прямоугольник со сторонами a , b уместить внутри прямоугольника со сторонами c , d так, чтобы каждая из сторон одного прямоугольника была параллельна или перпендикулярна каждой стороне второго прямоугольника.
Скачать решение на языке: TPascal
Задача №56 (Из учебника С.А. Абрамов, Г.Г. Гнездилова, Е.Н. Капустина, М.И. Селюн; Вологда 2000г.)
Даны действительные положительные числа a , b , c , x , y . Выяснить, пройдет ли кирпич с ребрами a , b , c в прямоугольное отверстие со сторонами x и y . Просовывать кирпич в отверстие разрешается только так, чтобы каждое из его ребер было параллельно или перпендикулярно каждой из сторон отверстия.
Скачать решение на языке: TPascal
Задача №57 (Из учебника С.А. Абрамов, Г.Г. Гнездилова, Е.Н. Капустина, М.И. Селюн; Вологда 2000г.)
Дано действительное число a . Вычислить f ( a ), если


Скачать решение на языке: TPascal
Задача №58 (Из учебника С.А. Абрамов, Г.Г. Гнездилова, Е.Н. Капустина, М.И. Селюн; Вологда 2000г.)
Дано действительное число a. Для функций f(x), графики которых представлены на рис. 1,a - 1,г, вычислить f(a).
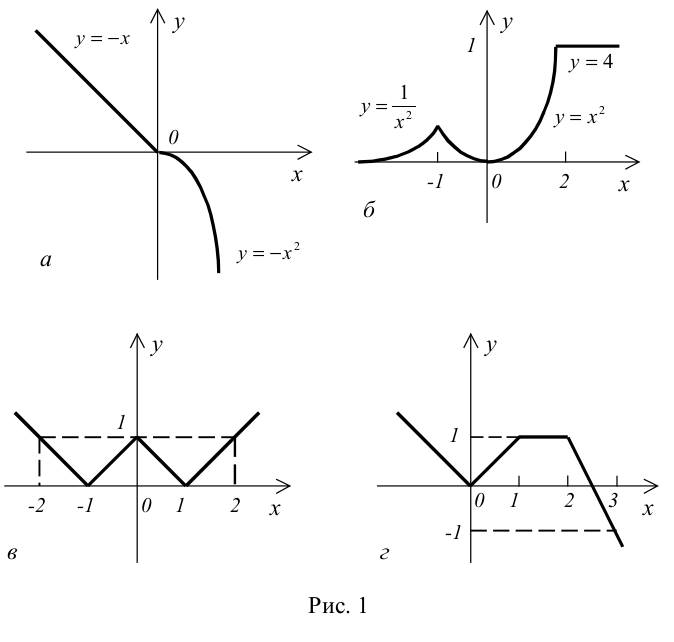
Скачать решение на языке: TPascal
Задача №59 (Из учебника С.А. Абрамов, Г.Г. Гнездилова, Е.Н. Капустина, М.И. Селюн; Вологда 2000г.)
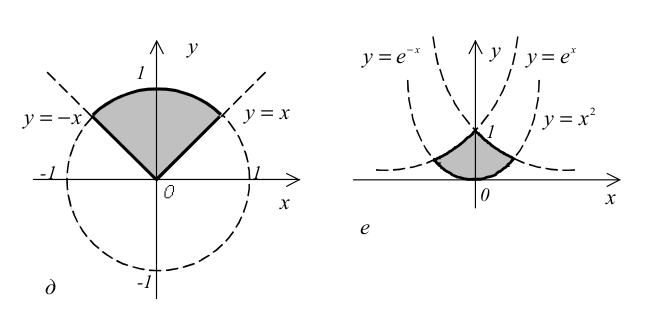
Даны действительные числа x , y . Определить, принадлежит ли точка с координатами x , y заштрихованной части плоскости
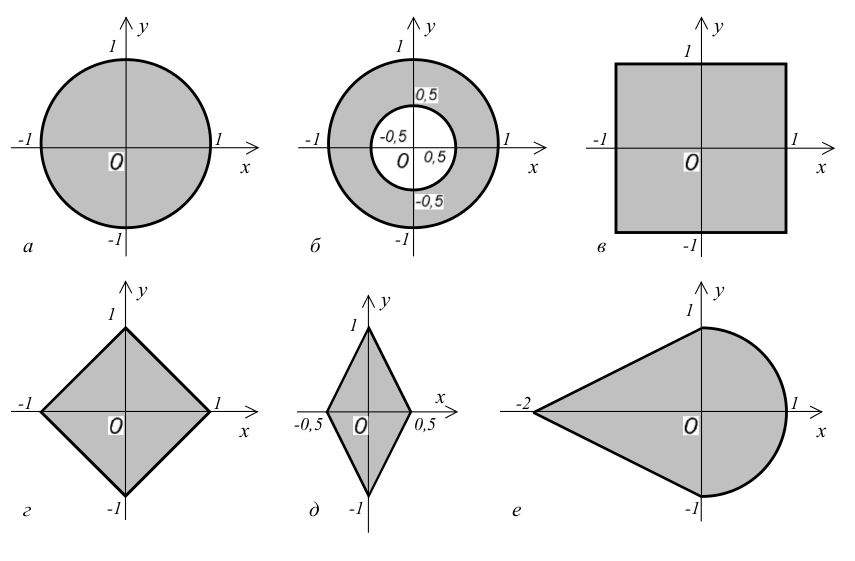
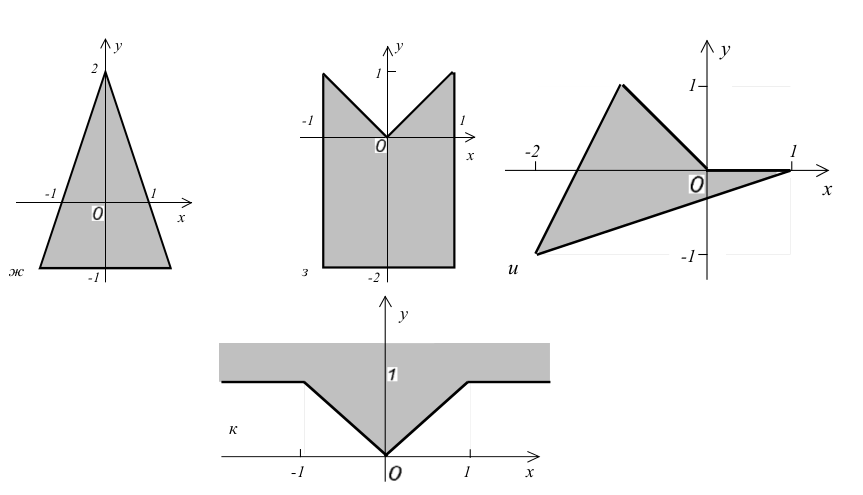
Скачать решение на языке: TPascal
Задача №60 (Из учебника С.А. Абрамов, Г.Г. Гнездилова, Е.Н. Капустина, М.И. Селюн; Вологда 2000г.)
Пусть D – заштрихованная часть плоскости (рис. 1, а —3, е ) и пусть u определяется по x и y следующим образом (запись ( x , y ) ∈ D означает, что точка с координатами x , y принадлежит D ):